Создание точки на кривой Безье

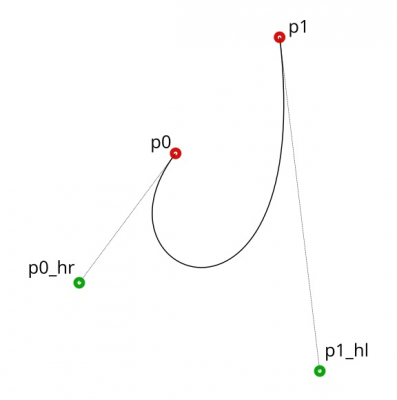
Кривая Безье строится по четырем точкам: две основные точки (p0, p1) и две опорные (p0_hr, p1_hl).

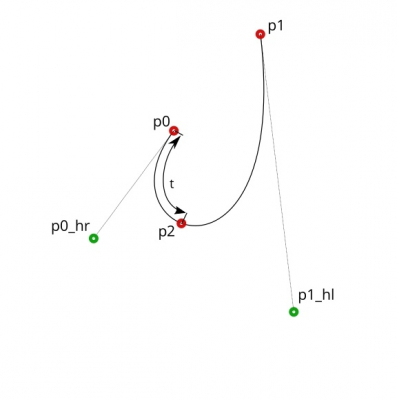
Для того, чтобы построить на кривой дополнительную точку p2 в какой-то момент t, где t изменяется от 0 до 1 и представляет собой соотношение положения строящейся точки p2 к общей длине кривой, нужно проделать следующие вычисления:

Имеющиеся исходные данные:

• координаты точек p0 и p1
• координаты правой опорной точки для p0 – р0_hr
• координаты левой опорной точки для p1 – p1_hl
• соотношение t

Нужно найти:

• координаты для новой точки p2
• координаты двух ее опорных точек (левой и правой)
• новые координаты для опорных точек p0_hr и p1_hl

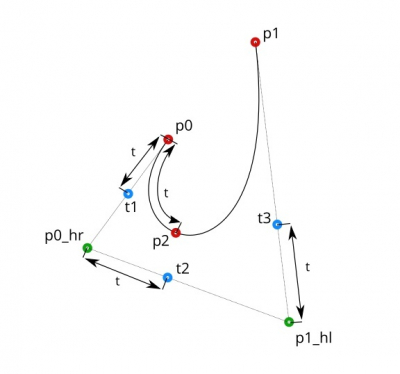
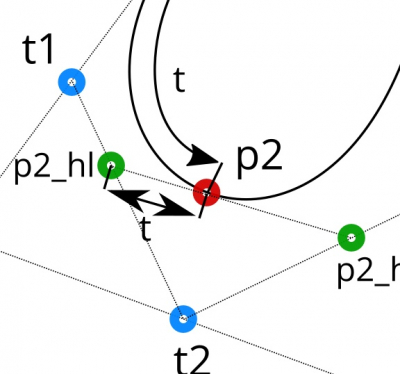
Разобьем отрезки [p0, p0_hr], [p0_hr, p1_hl] и [p1_hl, p1] точками t1, t2 и t3 в соотношении t по их длине.

Координаты построенных точек можно определить с помощью векторной математики, ведь координаты точки в пространстве – это вектор из начала координат (0,0,0) в эту точку.

На примере точки t1:

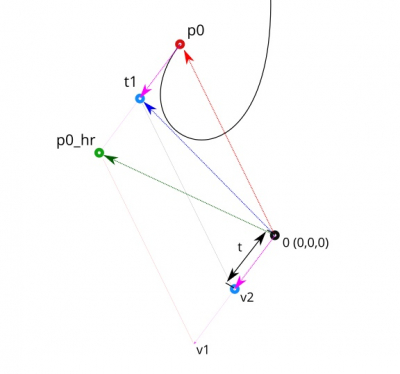Имея исходные вектора (p0) и (p0_hr), можно получить вектор (v1), как разность (p0) и (p0_hr):

Имея исходное соотношение t, можно получить вектор (v2):

Сумма векторов (v2) и (p0) даст нужный вектор t1:

И все вместе:

Аналогично для точек t2 и t3:

Полученные точки t1 и t3 – это координаты новых положений опорных точек для p0 и p1.

Нам осталось получить координаты точки p2 и двух ее опорных точек.

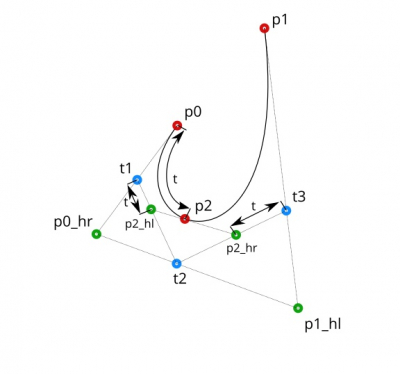
Соединим точки t1, t2 и t2, t3 отрезками. Теперь можно получить опорные точки для p2, исходя из все того же соотношения t.

Осталось найти координаты самой точки p2.

На отрезке, соединяющем точки p2_hl и p2_hr искомая точка p2 будет находится все по тому же соотношению t.

Выражения для нахождения всех нужных точек получены. Наконец мы можем оставить математику и написать функцию для нахождения дополнительной точки на кривой Безье со всеми необходимыми опорными точками.

Теперь добавим на кривую Безье новую точку и установим полученные координаты точек.