To mirror an object along X, Y or Z axis in Blender the “Miror” operator is usually used. For example, to mirror an object along the global X axis, in the 3D viewport window menu we need to select: Object – Miror – X Global. Or we can do it simpler just applying a scale of -1 to the object along the desired axis: s – x – -1. However, if there are custom normals on the object, they are not recalculated, which subsequently causes the appearance of various artifacts.
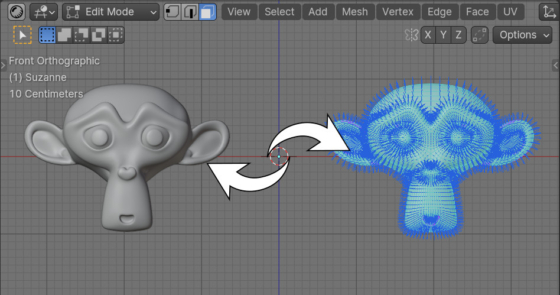
Let’s take the “Suzanne” object as an example and add custom normals to it. In the Properties area, open the Object Data tab and in the Geometry Data section, press the Add Custom Split Normals Data button. In the Modifiers tab, add the “NormalEdit” modifier to the object and set arbitrary values. Now, if we mirror an object in a standard way (s – x – -1) and apply a scale to it (Ctrl + a – Scale), it will be visually clear that normals was broken. At the same time, the “Mirror” modifier mirrors the object correctly, taking into account the custom normals.
We can mirror an object relative to the X axis with correct conversion of custom normals without using the “Mirror” modifier using the following script:
Original code author: Joey (blender.stackexchange).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import bpy me = bpy.context.object.data me.calc_normals_split() me.use_auto_smooth = True mirror_split_normals = [] for iter_poly in me.polygons: reverse_normals_indices = [iter_poly.loop_indices[0]] + list(reversed(iter_poly.loop_indices[1:])) for i in reverse_normals_indices: mirror_split_normals.append((me.loops[i].normal[0] * -1, me.loops[i].normal[1], me.loops[i].normal[2])) for v in me.vertices: v.co = v.co[0] * -1, v.co[1], v.co[2] me.flip_normals() me.normals_split_custom_set(mirror_split_normals) |
In this code
|
1 2 |
me.calc_normals_split() me.use_auto_smooth = True |
We first recalculate custom normals and enable the auto-smoothing mode, which is necessary to work with them.
Next, for each mesh polygon, we rotate all the loops in the opposite direction, leaving the starting point unchanged.
|
1 |
reverse_normals_indices = [iter_poly.loop_indices[0]] + list(reversed(iter_poly.loop_indices[1:])) |
After that, we mirror the normal on each loop relative to the X axis and save them in a separate list.
|
1 |
mirror_split_normals.append((me.loops[i].normal[0] * -1, me.loops[i].normal[1], me.loops[i].normal[2])) |
Actually mirror the mesh relative to the X axis:
|
1 2 |
for v in me.vertices: v.co = v.co[0] * -1, v.co[1], v.co[2] |
Flip the normals
|
1 |
me.flip_normals() |
And add recalculated custom normals, already reflected relative to the X axis.
|
1 |
me.normals_split_custom_set(mirror_split_normals) |
If we now apply scale to the mirrored mesh, to check custom normals, we will see that they are processed correctly.
For the same mirroring relative to other axes, we need to make minimal changes to the script in order to recalculate the required (Y or Z) component of the normals.
 .blend file on Patreon
.blend file on Patreon