To distribute objects with Blender Geometry Nodes, the “Distribute Points on Faces” node is usually used. It produces a set of points randomly scattered over the surface of the mesh polygons. Next, the necessary objects are located at these points. In common case, these points are located randomly, and the objects located on them can intersect with each other if the points are close. However, we can configure the nodes so that the meshes located on the points will not intersect.
Let’s add a plane to the scene (shift + a – Mesh – Plane), and append a Geometry Nodes modifier for it. By pressing the “New” button, create a new Geometry Nodes node tree.
Add a “Distribute Points on Faces” node (shift+a – Points – Distribute Points on Faces) to the node tree to get the points’ distribution on the plane.
Add an “Instance on Points” node (shift+a – Instance – Instance on Points) to locate objects to the received points.
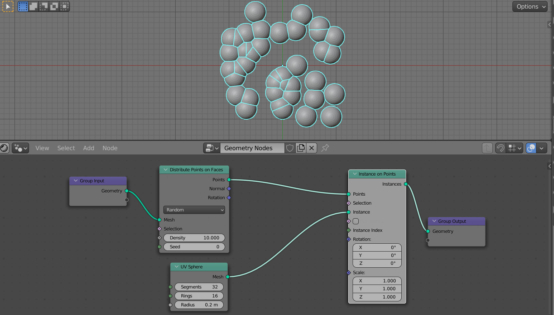
Now add a “UV Sphere” node (shift+a – Mesh Primitives – UV Sphere) and connect its “Mesh” output to the “Instance” input of the “Instance on Points” node. In the “Radius” field of the “UV Sphere” node, specify a value equal to 0.2.
So, the spheres are randomly distributed over the surface of the plane, but they intersect with each other.
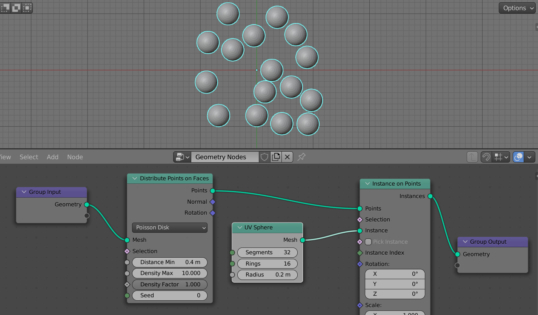
To solve the problem of object intersection, the “Distribute Points on Faces” node has a separate “Poisson Disk” mode. When it is enabled, points on the surface are still randomly arranged, but in such a way that the distance between two adjacent points is never less than the value specified in the “Distance Min” node field.
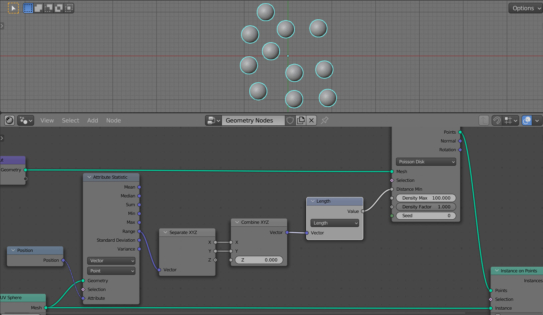
Switch the “Distribute Points on Faces” node to the “Poisson Disk” mode.
For our example, the minimum distance between the spheres so that they do not intersect with each other will be equal to the radius of the sphere multiplied by 2. Since we specified the radius of the sphere to be 0.2, we will specify the value 0.4 in the “Distance Min” field of the “Distribute Points on Faces” node.
All intersections are eliminated.
For objects more complex than a sphere, the minimum distance without intersections can be obtained, for example, using the “Bounding Box” node or, a bit more precisely, using the “Attribute Statistic” node.
Add an “Attribute Statistic” node (shift+a – Attribute – Attribute Statistic) to the node tree. Link its “Geometry” input with the “Geometry” output of the “UV Sphere” node, because we will seek the desired distance according to the object geometry.
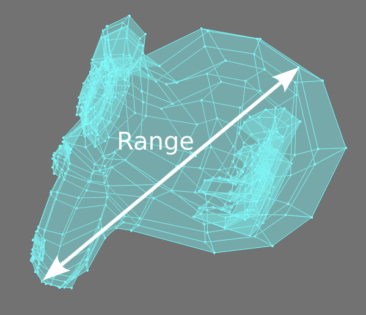
The “Attribute Statistic” node has a “Range” output that returns the largest distance between mesh points – just what we need.
Switch the node to the Vector – Point mode to get values from the “point” attribute of the vector type.
Add a “Position” node (shift+a – Input – Position) and link its “Position” output with the “Attribute” input of the “Attribute Statistic” node to collect statistics from the mesh’s vertices.
The vector obtained from the “Range” output is three-dimensional, but to control the distance between objects on the plane, we need only its projections onto the XY plane.
Let’s add Separate XYZ (shift+a – Vector – Separate XYZ) and Combine XYZ (shift + a – Vector – Combine XYZ) nodes to the tree and connect their inputs and outputs for the X and Y axes, leaving the Z axis unconnected. Link the Vector input of the Separate XYZ node with the Range output of the Attribute Statistic node. We will get the projection of the Range vector onto the XY plane.
To determine the distance between objects, we just need to take the length of this projection. Add a Vector Math node (shift + a – Vector – Math) and switch it to the Length mode. Link the Vector output of the Combine XYZ node with the Vector input of the Vector Math node.
The value obtained at the output of the Vector Math node is the maximum size of the object in the projection onto the XY plane. Link the node Value output with the Distance Min input of the Distribute Points on Faces node.
Now this set of nodes can be used with any objects of a more complex shape than a sphere, with no intersections.

 .blend file on Patreon
.blend file on Patreon