When we need to add several different objects to the scene, and at the same time, each object should appear in the scene with a greater or lesser probability, we can use the “random.choice” method for generating random sets from the Python “numpy” module.
First, let’s define a list of objects for adding to the scene. For example it could be spheres, cubes and Suzannes:
|
1 |
k = ['sphere', 'cube', 'monkey'] |
Let’s also define a list of probabilities with which these objects should appear in the scene:
|
1 |
ki = [0.6, 0.3, 0.1] |
The list of probabilities must contain the same number of elements as the list with objects. The number is the probability of an object appearing in the scene, which is in the list of objects in the same place.
In our case, for spheres, the probability of appearing is 0.6 (most often), for cubes – 0.3 (less often) and for Suzannes – 0.1 (rarely).
Convert the list of probabilities to a numpy array (numpy.array). And additionally normalize the values. It is needed if the sum of the probabilities we set in the list is not equal to 1 (for example, if we definde the probabilities in percentage format [60, 30, 10]).
|
1 2 3 4 |
import numpy as np p = np.array(ki) p /= p.sum() |
Now call the “random.choice” method to generate a set of 6 objects that we want to add to the scene.
|
1 2 3 4 5 6 |
rez = np.random.choice( a=k, size=6, replace=True, # False to make only unique choice p=p ) |
In the first parameter “a” we specified the initial list of objects.
We set the “size” parameter to 6. This means that as a result we want to get a list of six objects.
Since the number of objects we need is greater than in the original list, the “replace” parameter must be set to True. This means that we allow repetition of objects in the resulting list. If we set it to False, then each object from the source list will be present in the resulting list only once. However, in this case, we need to make sure that the length of the original list of objects is greater than or equal to the number specified in the “size” parameter.
In the “p” parameter, we specify a numpy array with normalized probabilities.
If we execute our code several times and print the resulting list,
|
1 2 3 4 5 6 7 8 9 |
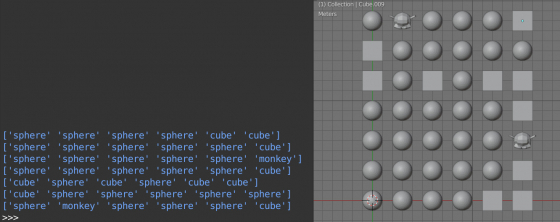
print(rez) # ['sphere' 'sphere' 'sphere' 'sphere' 'cube' 'cube'] # ['sphere' 'sphere' 'sphere' 'sphere' 'sphere' 'cube'] # ['sphere' 'sphere' 'sphere' 'sphere' 'sphere' 'monkey'] # ['sphere' 'sphere' 'sphere' 'sphere' 'sphere' 'cube'] # ['cube' 'sphere' 'cube' 'sphere' 'cube' 'cube'] # ['cube' 'sphere' 'sphere' 'sphere' 'sphere' 'sphere'] # ['sphere' 'monkey' 'sphere' 'sphere' 'sphere' 'cube'] |
we can clearly seen that, spheres are most common, cubes are much rarer, and Susannas are very rare as required.

 .blend file on Patreon
.blend file on Patreon