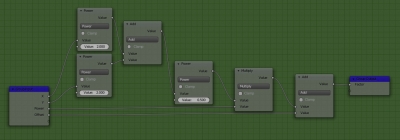
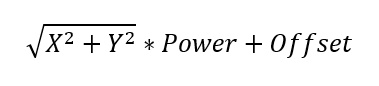Except for the “Gradient Texture” node, we can obtain a gradient factor by using some simple equations. Look for the mathematics with a spherical gradient sample.
- Uniform gradient
Can be created based on a downward-facing cone equation.
X, Y – input coordinate vector components
Power – tilt angle
Offset – cone offset along the Z-axis
Make it with nodes:
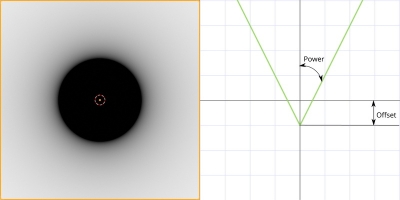
That gradient has the transition area from 0 (black) to 1 (white) always uniform. The “Offset” can be used to quickly resize the black area in the center. The “Power” factor also affects the black area size, but more significantly affects the width of the gradient area.
- Quadratic gradient
Based on the parabola equation.
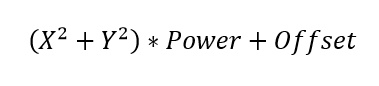X, Y – input coordinate vector components
Power – parabolic steepness
Offset – parabola offset along the Z-axis
Make it with nodes:
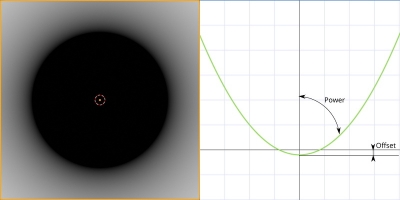
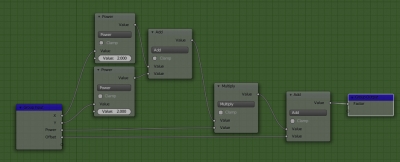Due to the parabola shape, the gradient transition region does not uniform in width. It is lighter on the inner edge and harder on the outer edge of the junction. The “Power” and the “Offset” coefficients are also responsible for the width of the gradient region and the size of the zero region in the center.