Let’s fill the curve with the required number of objects so that they occupy the entire length of the curve without gaps, adjusting their scale if necessary.
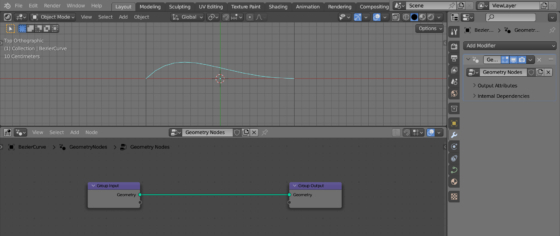
Open an empty blend-file. Add a curve (shift + a – Curve – Bezier). Append the Geometry Nodes modifier to it and initialize the initial node tree.
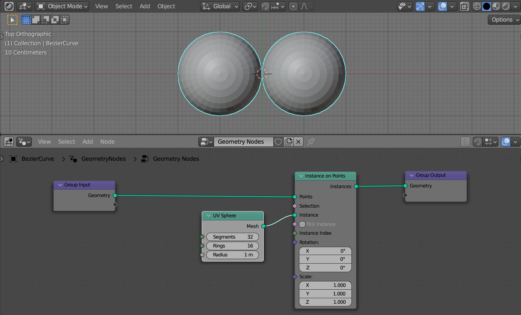
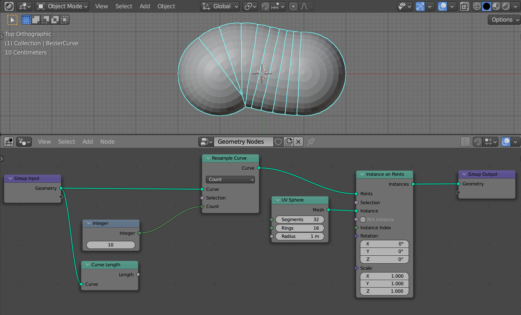
Let’s fill the curve, for example, with spheres.
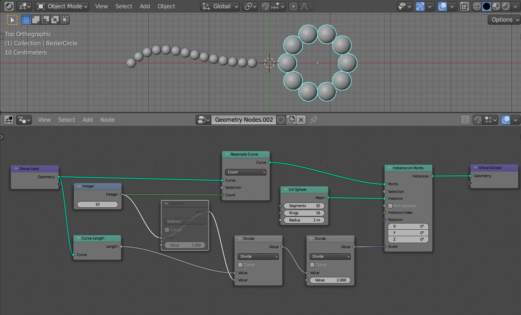
Add an Instance On Points (shift + a – Instance – Instance On Points) node to the main branch of the node tree – this node is responsible for placing the mesh at each point of the curve.
Add a UV Sphere node (shift + a – Mesh Primitives – UV Sphere) and link its Mesh output with the Instance input of the Instance On Points node. Thus, at each point of the curve, we placed a UV Sphere mesh.
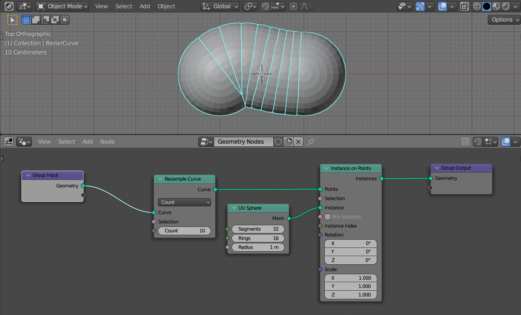
Our curve consists of only two points. Let’s increase the number of points on the curve using the Resample Curve node (shift + a – Curve – Resample Curve), adding it to the very beginning of the main branch of the node tree.
Now there are 10 points on our curve, and in each of them there is a UV Sphere mesh instance.
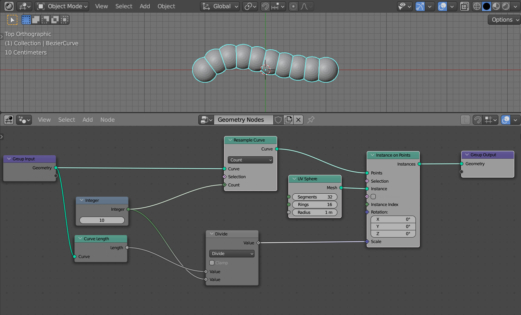
Let’s make the scale of the sphere independently adjusts to the number of points on the curve so that the spheres do not intersect.
To get the scaling factor for the spheres, we need to divide the length of the curve by the number of its points. This will give us the distance between two points on the curve – the desired size of the mesh.
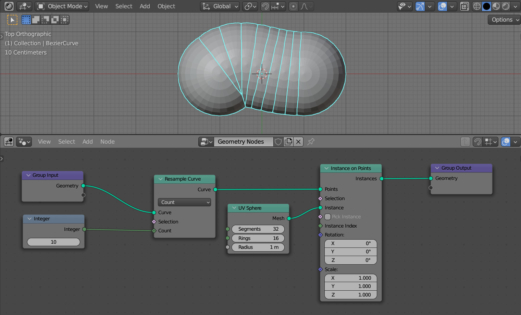
Separate the number of points on the curve to the single node. Add an Integer node (shift + a – Input – Integer), set its value to 10, and link its Integer output with the Count input of the Resample Curve node.
We can get the curve length using the Curve Length node (shift + a – Curve – Curve Length). Add it to the node tree. Link its Curve input with the Geometry output of the Geometry Output node. From its Length output, we can now take the length of our curve.
Add a Math node (shift + a – Utilities – Math) and switch it to the Divide mode. Link its upper Value input with the Length output of the Curve Length node, and its lower input with the Integer output of the Integer node. Thus, we divide the curve length by the number of its points.
Link the Value output of the Math node with the Scale input of the Instance On Points node, to set the scale coefficient depending on curve length and number of its points.
As we can see, the spheres have decreased, but clearly not enough.
Since the size of the sphere is given by the radius, and when filling the curve, the full sphere – its diameter is used, the scaling factor that we got must be divided by 2.
Add another Math node (shift + a – Utilities – Math) in Divide mode. Insert it between the existing Divide node and the Instance On Points node. The value of the lower Value input, which remains free, set to 2.
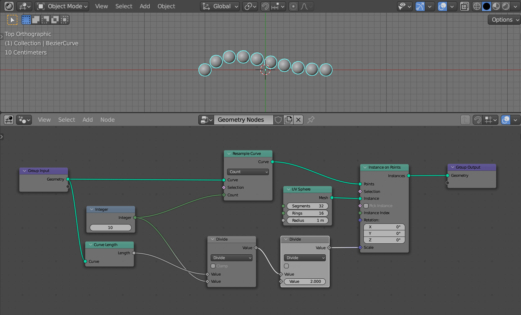
The spheres are now scaled beauty to fill the entire curve. By changing the value in the Integer node, we can easily control the number of spheres.
However, with a few spheres number, some gaps appears. The artifact appears due to the fact that we filled the curve based on the number of points on it, but it is necessary to fill in the gaps between the points. Since the spheres placed on two extreme points on the curve will half crawl out.
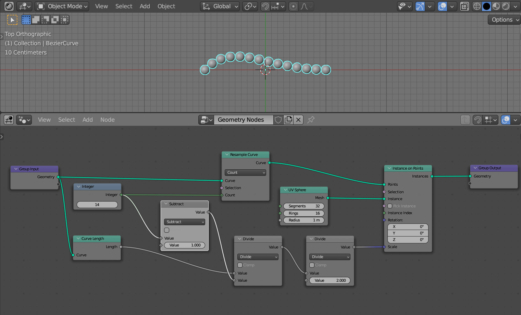
The number of gaps between points is always one less than the number of points. Therefore, to achieve final accuracy, we just need to subtract 1 from the number of points when calculating the scale factor for spheres.
Add another Math node (shift + a – Utilities – Math) and switch it to the Subtract mode. Place it between the Integer node and the first Divide node.
Set to 1 the value of the lower Value input.
The spheres are now scaled exactly along the length of the curve.
It should be noted that for closed curves, the last action is not required. This happens because in a closed curve, the last point always coincides with the first.
For closed curves, the subtraction node can be “muted” – excluded from the calculation, by selecting it and pressing the “m” key.

 .blend file on Patreon
.blend file on Patreon