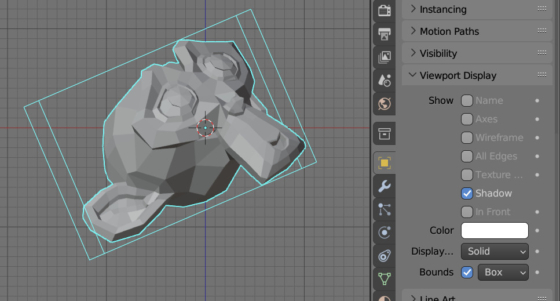
For quick and rough checking of two objects geometry intersections, bounding objects are usually used – spheres or parallelograms in which all points of the object are inscribed. Bounding object intersections are often inaccurate, but they are very efficient in terms of speed. One of the types of bounding objects is AABB (Axis Aligned Bounding Box) – a parallelogram aligned with the global coordinate axes.
Each object in Blender always has a bounding box already calculated. It can be seen in the 3D Viewport area by checking the “Bounds” checkbox in the Object Properties panel in the Properties area. But this parallelogram is not aligned with the global axes, which makes it slightly slower in calculations.
For an axis-aligned bounding box (AABB), we can calculate the required points ourselves.
At first, we need to recalculate all object vertices coordinates into the global coordinate system by multiplying their local coordinates by the world matrix of the object.
|
1 2 3 |
obj = bpy.context.object vertices_world = [obj.matrix_world @ vertex.co for vertex in obj.data.vertices] |
Now let’s define a function to find the minimum and maximum values of the coordinates along the X, Y and Z axes. The function will return us the coordinates of two points at the ends of the main AABB diagonal.
|
1 2 3 4 5 6 7 8 9 10 |
def _aabb(vertices_cloud): x, y, z = zip(*(p for p in vertices_cloud)) return { "min_x": min(x), "min_y": min(y), "min_z": min(z), "max_x": max(x), "max_y": max(y), "max_z": max(z) } |
In the function parameter, we pass a list of coordinates of the object’s vertices in the global coordinate system.
Inside the function, we first split the list of vertices coordinates into three separate lists, in which we placed separately the coordinates along the X, Y and Z axes.
The minimum and the maximum values in each of the lists will be the coordinates of the end points of the main AABB diagonal that we are looking for.
|
1 2 3 4 5 |
aabb = _aabb(vertices_world) print(aabb) # {'min_x': -1.2374733686447144, 'min_y': -1.0057023763656616, 'min_z': -1.158319115638733, # 'max_x': 1.0172135829925537,'max_y': 1.2093106508255005,'max_z': 0.8847196698188782} |
The coordinates of these two points of AABB are enough to get the coordinates of all its other points.
Let’s create an object in the scene built according to the obtained coordinates.
Define the “vertices” list with eight AABB vertices coordinates and the “edges” list – set of vertices indices to build edges:
|
1 2 3 4 5 6 7 8 9 10 11 |
vertices = [ (aabb['min_x'], aabb['min_y'], aabb['min_z']), (aabb['max_x'], aabb['min_y'], aabb['min_z']), (aabb['max_x'], aabb['max_y'], aabb['min_z']), (aabb['min_x'], aabb['max_y'], aabb['min_z']), (aabb['min_x'], aabb['min_y'], aabb['max_z']), (aabb['max_x'], aabb['min_y'], aabb['max_z']), (aabb['max_x'], aabb['max_y'], aabb['max_z']), (aabb['min_x'], aabb['max_y'], aabb['max_z']) ] edges = [(0,1), (1,2), (2,3), (3,0), (4,5), (5,6), (6,7), (7,4), (0,4), (1,5), (2,6), (3,7)] |
Create a mesh according to the defined geometry and add it to the scene:
|
1 2 3 4 5 |
new_mesh = bpy.data.meshes.new('AABB') new_mesh.from_pydata(vertices, edges, faces) new_mesh.update() aabb = bpy.data.objects.new('new_object', new_mesh) bpy.context.collection.objects.link(aabb) |
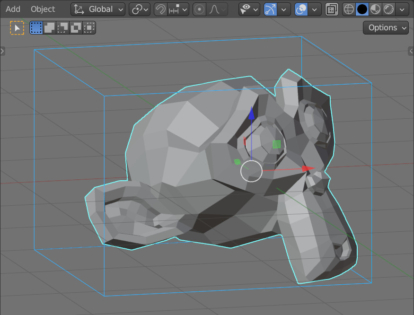
Now we clearly see that the bounding parallelogram built according to our calculations completely fits into the original object and is aligned with the global coordinate axes. So this parallelogram is the real AABB for the initial object.
 .blend file on Patreon
.blend file on Patreon