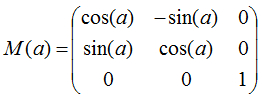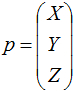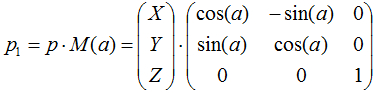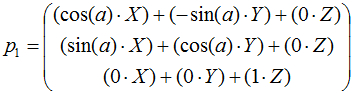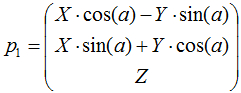Для того, чтобы добиться нужного расположения текстуры на поверхности объекта необходимо иметь удобный инструмент для манипуляций с текстурными координатами. Особенно, если текстура процедурная и наложена на объект без использования развертки.
Нод Mapping, совмещающий в себе инструменты перемещения, вращения и изменения масштаба текстуры, покрывает большинство задач текстурирования. Однако часто его возможностей недостаточно. Его основной недостаток в том, что он позволяет задавать значения для регулировки только в определенных полях внутри самого нода. Эти поля не имеют выходов наружу и к ним нельзя подсоединить связи от других нодов дерева.
При помощи связки других нодов можно реализовать нужный функционал, лишенный недостатка нода Mapping. Рассмотрим, как построить связку нодов для вращения текстуры вокруг оси Z объекта на случайную величину.
- Подготовим сцену:
- Добавим сферу, назначим ей модификатор Subdivision Surface для сглаживания и в T-панели переключим отображение полигонов в режим Smooth.
- Перейдем в режим просмотра “сверху”. Теперь ось Z смотрит перпендикулярно монитору.
- Назначим сфере простейший материал по умолчанию (Diffuse 0.8).
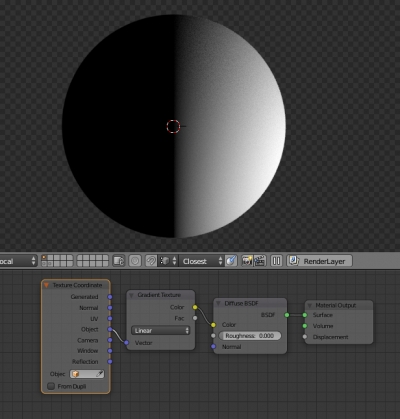
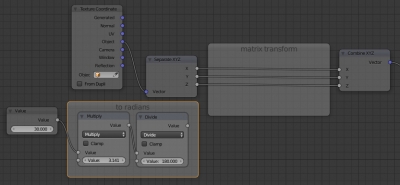
- В окне материала (Node Editor) мы будем производить построение нужной связки нодов:
- Для наглядности добавим нод Gradient Texture и соединим его выход Color со входом Color нода Diffuse.
- Добавим так же нод Texture Coordinate и соединим его выход Object со входом Vector нода Gradient Texture.
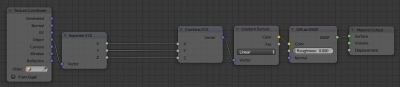
Должна получиться следующая заготовка для дальнейшей работы:
Итак, нам нужно повернуть текстуру Gradient Texture вокруг оси Z сферы.
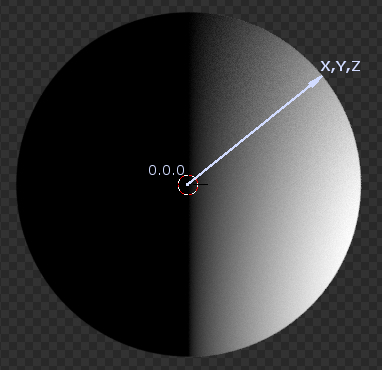
В качестве системы координат для текстуры Gradient Texture мы задали Object сферы. Поэтому начальная точка для расчета текстуры совпадает с центральной точкой (Origin) сферы, а вектор из начальной точки в любую точку поверхности сферы будет являться вектором, определяющим значение (цвет) текстуры в этой точке.
Это значит, что для того, чтобы повернуть текстуру вокруг оси Z сферы, нам нужно повернуть вокруг центральной точки (0,0,0) все вектора (0,0,0 – X,Y,Z), которые мы получаем с выхода Object нода Texture Coordinate.
Наилучший способ манипуляций векторами в пространстве – матричные трансформации. Если не углубляться в теорию, основной принцип можно сформулировать так: если вектор, имеющий заданные координаты в пространстве умножить на определенную матрицу, в результате будет получен новый вектор, перемещенный, повернутый или изменивший свой масштаб.
Матрица вращения вектора вокруг оси Z в трехмерном пространстве имеет следующий вид:
где a – угол в радианах, на который будет выполнен поворот.
Исходный вектор
мы получаем с выхода Object нода Texture Coordinate.
Для того, чтобы повернуть вектор, нужно умножить его на матрицу:
Сверившись с правилами умношения вектора на матрицу, получим следующий результат:
Или немного упрощая:
Получив нужную формулу, можно отложить в сторону учебник математики и вернуться в Blender.
Как мы выяснили, исходный вектор p(X,Y,Z) мы получаем на выходе Object нода Texture Coordinate. Для того, чтобы получить доступ к его координатам по отдельности, добавим в дерево нодов новый нод Separate XYZ, который позволяет разделить вектор на его координатные составляющие. Так как после окончания преобразований нам опять понадобиться целый вектор (для входа Vector нода Gradient Texture), добавим также нод Combine XYZ, который позволяет собрать вектор из составляющих.
Соединив соответствующие входы и выходы нод, получим следующее дерево:
В промежутке между нодами Separate XYZ и Combine XYZ мы будем строить всю “математику”.
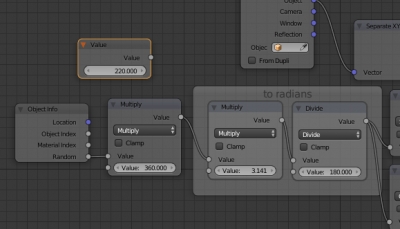
Добавим новый нод Value. Здесь мы будем задавать значение основной переменной a – угла поворота в градусах. Но так как полученная выше формула требует угла в радианах, преобразуем задаваемое значение, умножив его на π и поделив на 180.
В полученной выше формуле угол поворота не используется в чистом виде, нужны только синус и косинус этого угла. Добавим два нода для получения синуса и косинуса.
Осталось для каждой координаты вектора произвести математические вычисления.
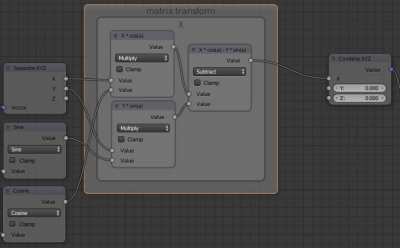
Для координаты X: добавляем два нода умножения для получения произведений X*cos(a) и Y*sin(a) и нод вычитания второго произведения из первого. В результате реализуется формула X*cos(a)-Y*sin(a).
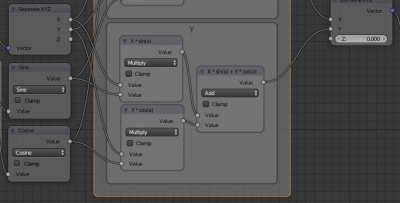
Так же реализуем нодами формулу для координаты Y.
Значение координаты Z не меняется, поэтому просто соединяем соответствующий выход Separate XYZ со входом Combine XYZ.
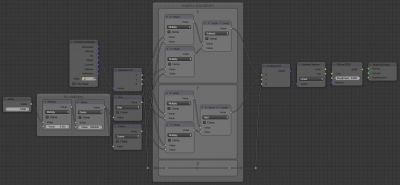
Итоговое дерево нодов выглядит так:
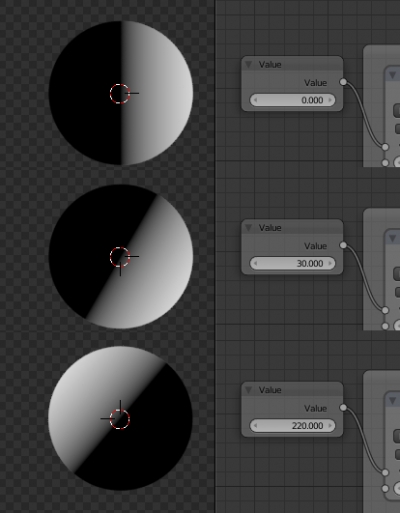
Меняя значение нода Value можно визуально наблюдать, как поворачивается текстура на сфере.
Но просто поворачивать текстуру мы могли и при помощи нода Mapping. Реализуем поворот текстуры на случайную величину.
Для этого отсоединим нод Value от задания угла поворота. На его место добавим нод Object Info. У этого нода есть выход Random, который генерирует случайную величину в диапазоне от 0 до 1. Т.к. угол поворота меняется в диапазоне от 0 до 360 градусов, добавим нод, умножающий случайное значение, взятое с выхода Random на 360. Результат используем для задания угла поворота a.
А теперь создадим еще несколько сфер, назначив им всем созданный материал.