Для быстрого и грубого определения пересечений геометрии двух объектов обычно используются ограничивающие объекты – сферы или параллелограммы в которые вписаны все точки объекта. Хотя просчет пересечений по ограничивающим объектам часто бывает неточен, он очень эффективен по скорости работы. Одним из видов ограничивающих объектов является AABB (Axis Aligned Bounding Box) – параллелограмм, выровненный по глобальным осям координат.
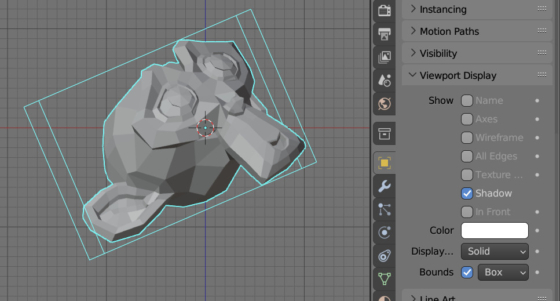
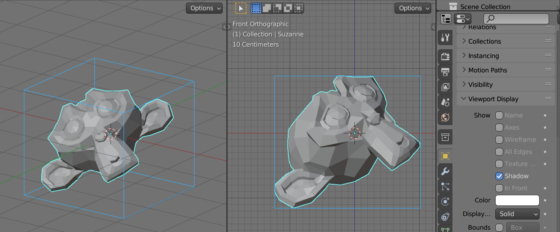
У каждого объекта в Blender всегда есть уже просчитанный ограничивающий параллелограмм – BB (Bounding Box). Его можно увидеть в окне 3D вьюпорта, отметив галочку Bounds в панели Object Properties в рабочей области Properties.
Однако, этот параллелограмм не выровнен по глобальным осям, что делает расчеты с ним чуть-чуть медленнее.
Для выровненного по осям ограничивающего параллелограмма мы можем самостоятельно рассчитать нужные точки.
Для начала координаты всех точек меша, для которого мы будем рассчитывать AABB, переведем в глобальную систему координат, умножив локальные координаты точки на мировую матрицу объекта.
|
1 2 3 |
obj = bpy.context.object vertices_world = [obj.matrix_world @ vertex.co for vertex in obj.data.vertices] |
Теперь определим функцию для поиска минимального и максимального значения координат по осям X, Y и Z. Функция вернет нам координаты двух точек, которые лежат на концах главной диагонали AABB.
|
1 2 3 4 5 6 7 8 9 10 |
def _aabb(vertices_cloud): x, y, z = zip(*(p for p in vertices_cloud)) return { "min_x": min(x), "min_y": min(y), "min_z": min(z), "max_x": max(x), "max_y": max(y), "max_z": max(z) } |
В параметре функции мы передаем список координат точек объекта в глобальной системе координат.
Внутри функции мы сначала разбили список координат точек на три отдельных списка, в каждый из которых поместили отдельно координаты по X, Y и Z осям.
Минимальные и максимальные значения в каждом из списков и будут искомыми нами координатами конечных точек главной диагонали AABB.
|
1 2 3 4 5 |
aabb = _aabb(vertices_world) print(aabb) # {'min_x': -1.2374733686447144, 'min_y': -1.0057023763656616, 'min_z': -1.158319115638733, # 'max_x': 1.0172135829925537,'max_y': 1.2093106508255005,'max_z': 0.8847196698188782} |
Координат этих двух точек AABB достаточно, для того чтобы получить координаты всех остальных его точек.
Для наглядности создадим в сцене объект, построенный по полученным координатам.
Определим список с восемью точками для AABB в список vertices и набор индексов точек для построения ребер в список edges:
|
1 2 3 4 5 6 7 8 9 10 11 |
vertices = [ (aabb['min_x'], aabb['min_y'], aabb['min_z']), (aabb['max_x'], aabb['min_y'], aabb['min_z']), (aabb['max_x'], aabb['max_y'], aabb['min_z']), (aabb['min_x'], aabb['max_y'], aabb['min_z']), (aabb['min_x'], aabb['min_y'], aabb['max_z']), (aabb['max_x'], aabb['min_y'], aabb['max_z']), (aabb['max_x'], aabb['max_y'], aabb['max_z']), (aabb['min_x'], aabb['max_y'], aabb['max_z']) ] edges = [(0,1), (1,2), (2,3), (3,0), (4,5), (5,6), (6,7), (7,4), (0,4), (1,5), (2,6), (3,7)] |
Создадим меш по заданной в списках геометрии и добавим его в сцену:
|
1 2 3 4 5 |
new_mesh = bpy.data.meshes.new('AABB') new_mesh.from_pydata(vertices, edges, faces) new_mesh.update() aabb = bpy.data.objects.new('new_object', new_mesh) bpy.context.collection.objects.link(aabb) |
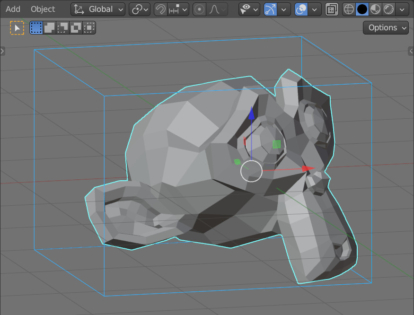
Теперь мы наглядно видим что построенный по нашим расчетам ограничивающий параллелограмм полностью вписывает в себя изначальный объект и выровнен по глобальным осям координат.
 .blend file on Patreon
.blend file on Patreon