Все процедурные текстуры в Blender основаны на математике. Даже такие нерегулярные структуры, как Voronoi и Noise, на самом деле сгенерированы по четким математическим формулами. Внутри каждого базового нода из редактора материалов Blender зашит точный математический алгоритм, в результате работы которого и получается нужное изображение.
Задать подобный алгоритм в привычной математической записи в Blender нельзя. Однако среди прочих нодов Blender предоставляет пользователю ноды группы Math – оболочку над простейшими математическими операциями. С помощью этих нодов можно самостоятельно строить сложные математические алгоритмы, генерирующие интересные текстуры.
Для примера сгенерируем текстуру с изображением простого круга.
Подготовим сцену:
Добавим плоскость
shift+a – Mesh – Plane
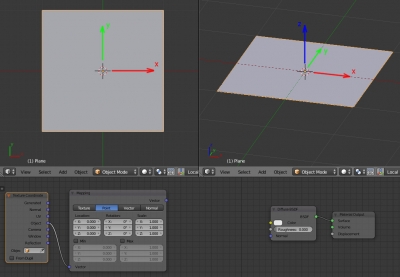
на которую будем проецировать создаваемую текстуру. Назначим ей дефолтный материал. В редакторе материалов Node Editor, кроме уже имеющихся нодов, добавим ноды Texture Coordinates и Mapping:
shift+a – Input – Texture Coordinate
shift+a – Vector – Mapping
Соединим выход Object нода Texture Coordinate со входом Vector нода Mapping. Таким образом мы назначаем плоскости систему координат Object, что означает, что центр координат накладываемой текстуры будет совпадать с центом Origin плоскости, а координатные оси текстуры будут направлены так же, как оси плоскости.
Теперь обратим внимание на то, какими исходными данными мы располагаем. Это значения трех координаты X, Y и Z в трехмерном пространстве, которые мы получаем с выхода Vector нода Mapping.
Все процедурные текстуры – трехмерные и описываются не двумя координатами, а тремя. Поэтому в сущности нам нужно построить не круг на плоскости, а сферу в трехмерном пространстве. Сечение сферы по оси Z даст нужный нам круг.
Настало время взять в руки справочник по математике и поискать формулу, связывающую имеющиеся у нас данные о координатах X, Y и Z с необходимой нам формой сферы. Формула легко находится:
Теперь нужно воссоздать эту формулу при помощи нодов в редакторе Node Editor.
Добавим нод, разбивающий Vector на отдельные координаты X, Y, Z:
shift+a – Converter – Separate XYZ
и соединим его с нодом Mapping. Теперь мы имеем доступ к координатам, нужным для построения формулы.
Последовательно по действиям воссоздадим формулу при помощи нодов.
Добавим нод Math:
shift+a – Converter – Math
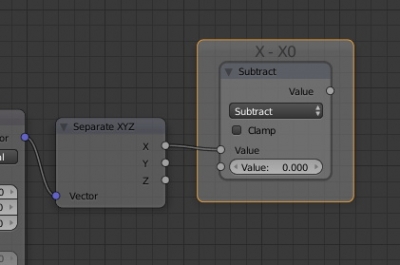
и переключим его в режим вычитания Subtract. В этом режиме из верхнего входящего значения нода вычитается нижнее значение. На верхний вход подадим координату X, нижний вход сделаем равным нулю (X0 = 0) чтобы круг строился из начала координат. Таким образом мы задали часть формулы X – X0.
Добавим еще один нод Math и переключим его в режим Power – возведение в степень. На верхний вход подадим значение Value нода Subtract, нижнее установим равным 2. Таким образом мы возводим X – X0 в квадрат.
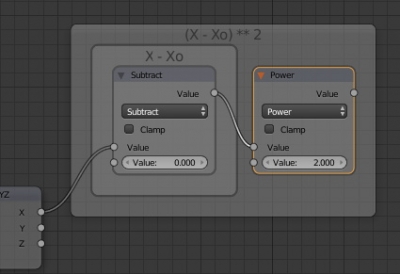Сделаем такие же группы для координат Y и Z.
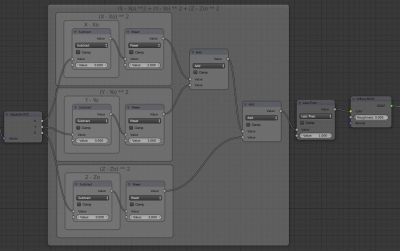
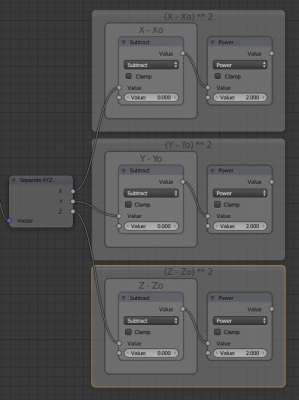Для того, чтобы сложить все три части уравнения, добавим еще два нода Math, переключив их в режим Add. Подключим к ним последовательно блоки для всех трех координат.
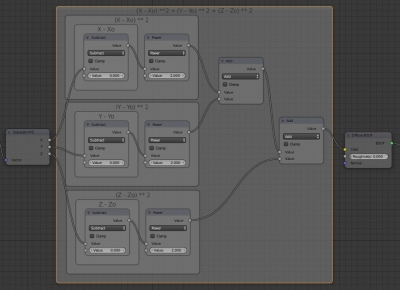Подключим выход последнего нода на вход Color нода Diffuse и в окне 3D_View перейдем в режим Rendered для просмотра результата.
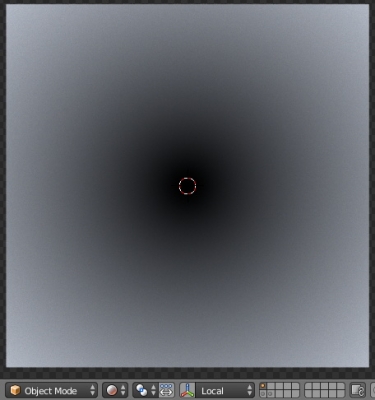Мы получили искомый круг, но он выглядит размытым. Это потому, что мы никак не ограничили правую часть уравнения – радиус.
Между нодом Duffuse и последним нодом Add вставим еще один нод Math и переключим его в режим Less Than. На верхний вход подадим значение нода Add, а второй установим равный 1. Теперь результат вычислений меньший единицы будет равен 1, а все, что больше – равно 0. Таким образом мы получаем точный процедурный круг с радиусом 1.
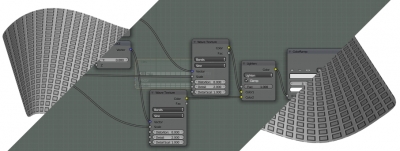
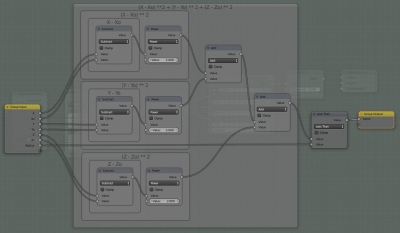
Итоговое дерево нодов выглядит так:
Для удобства можно объединить всю математику в группу
ctrl+g
и использовать получившуюся процедурную текстуру с кругом в своих рендерах.
Управлять расположением и размером круга также можно меняя значения в ноде Mapping.