При проверке коллизий в 2D проекциях между точкой и полигоном необходимо выяснить, лежит ли точка внутри полигона, или же она расположена вне его площади.
Для примера создадим криволинейный полигон (n-gon) любой формы под именем “Plane” и отдельно меш под именем Point, состоящий всего из одной точки.
Указатели на полигон и точку, будут определяться следующим образом:
|
1 2 |
polygon = bpy.data.objects['Plane'] point = bpy.data.objects['Point'] |
Для того чтобы определить, лежит ли точка point внутри полигона polygon, воспользуемся следующим алгоритмом:
- Пройдем последовательно по всем ребрам полигона;
- Для каждого ребра полигона проверим, лежит ли точка слева или справа от него;
- Если в результате всех проверок точка лежит справа от ребра четное количество раз – точка находится внутри полигона;
- Если точка лежит справа от ребер нечетное количество раз – точка находится вне полигона
- Если точка лежит на одном из ребер – сразу считает что точка находится внутри полигона.
Напишем этот алгоритм для проекции на плоскость XY.
Для начала нам нужно получить координаты всех точек полигона в порядке из следования друг за другом. Используем для этого функцию points_sorted().
|
1 2 3 4 |
poly_co = [(p.co.x, p.co.y) for p in points_sorted(polygon)] print(poly_co) # [(-1.0, -1.0), (-1.0, 1.0), (0.28521132469177246, 0.030281662940979004), ...] |
Координаты точки:
|
1 2 3 4 |
v_co = point.data.vertices[0].co.x, point.data.vertices[0].co.y print(v_co) # (0.16733169555664062, 0.4590986371040344) |
Если ориджины полигона и проверяемой точки не лежат в центре координат (0.0, 0.0, 0.0), нужно дополнительно привести все координаты к глобальной системе координат – умножить на матрицу мира matrix_world.
Определим функцию, которая в параметрах будет получить список координат полигона, отсортированный в нужном порядке и координаты точки, а на выходе возвращать 1, если точка находится внутри полигона, или 0 если она лежит вне полигона.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
def is_inside_polygon(polygon, point): length = len(polygon)-1 dy2 = point[1] - polygon[0][1] intersections = 0 ii = 0 jj = 1 # for each edge while ii<length: dy = dy2 dy2 = point[1] - polygon[jj][1] # check edges which are not completely above/bellow/right from the point if dy*dy2 <= 0.0 and (point[0] >= polygon[ii][0] or point[0] >= polygon[jj][0]): # non-horizontal edge if dy<0 or dy2<0: F = dy*(polygon[jj][0] - polygon[ii][0])/(dy-dy2) + polygon[ii][0] if point[0] > F: # if edge is left from the point - the ray moving towards left, will intersect it intersections += 1 elif point[0] == F: # point on edge return 2 # point on upper peak (dy2=dx2=0) or horizontal edge (dy=dy2=0 and dx*dx2<=0) elif dy2==0 and (point[0]==polygon[jj][0] or (dy==0 and (point[0]-polygon[ii][0])*(point[0]-polygon[jj][0])<=0)): return 2 ii = jj jj += 1 return intersections & 1 |
Теперь мы можем вызвать нашу функцию и предать в нее полученные ранее данные с координатами точек полигона и проверяемой точки:
|
1 2 3 4 |
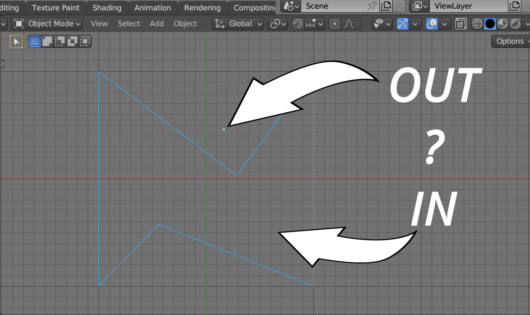
rez = is_inside_polygon(poly_co, v_co) print('IN' if rez else 'OUT') # OUT |
В нашем примере точка лежит вне полигона. Можно передвинуть ее в любое другое место (в режиме редактирования, если координаты не пересчитываются в глобальную систему) и снова сделать проверку.
 .blend file on Patreon
.blend file on Patreon