Doo-Sabin mesh subdivision based on a generalization of bi-quadratic uniform B-splines, as opposed to the more commonly used Catmull-Clark subdivision, which is based on generalized bi-cubic uniform B-splines. We can create a Doo-Sabin mesh subdivision using Blender Geometry Nodes with just two nodes.
.blend file on Patreon
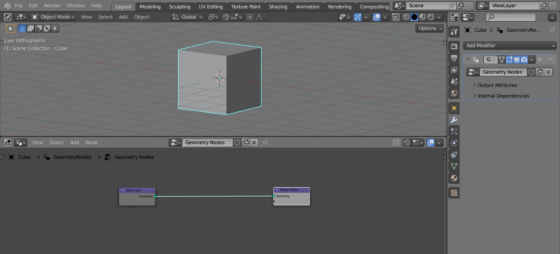
Add a cube to the scene (shift + a – Mesh – Cube), append the Geometry Nodes modifier to it and create an initial tree of nodes.
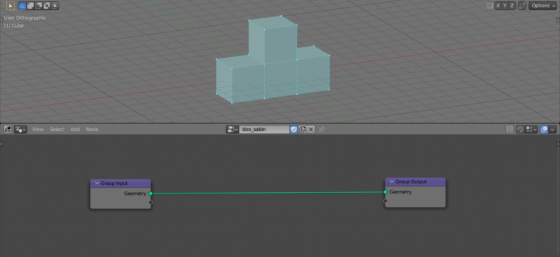
Let’s slightly complicate the shape of the mesh for clarity by extruding 3 faces of the cube in different directions (select face – e – 2 – enter).
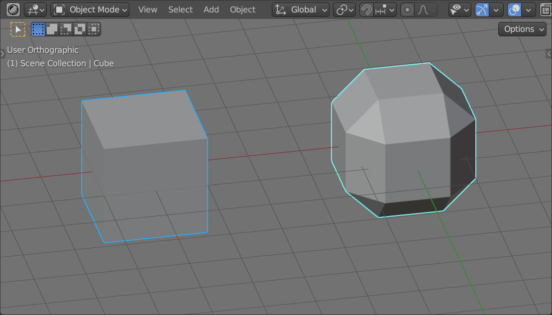
According to the Doo-Sabin algorithm, a subdivision must create a new face on every original vertex, a new face on every original edge, and a new face on every original face.
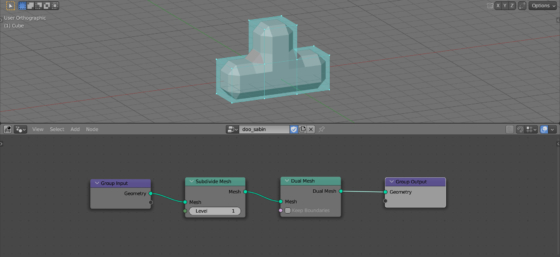
We can get the desired result using the Subdivide Mesh and Dual Mesh nodes.
Let’s add two nodes sequentially to the main branch of the node tree: Subdivide Mesh (shift + a – Mesh – Operators – Subdivide Mesh) and Dual Mesh (shift + a – Mesh – Operators – Dual Mesh).
This simple combination of nodes does all the necessary work – the result we get matches the algorithm.
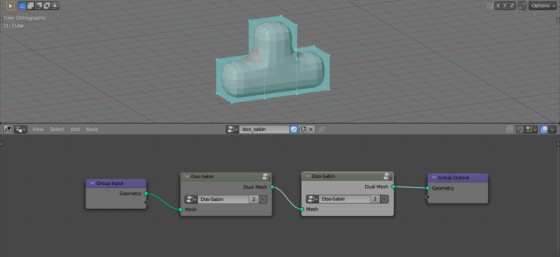
To make several levels of mesh subdivision, select both Subdivide Mesh and Dual Mesh nodes and press the Ctrl + g key combination to pack them into a group. Let’s name it “Doo-Sabin”.
Now, if we need to make a Doo-Sabin subdivision into 2 levels, we can simply add the node group we created sequentially twice to the main geometry branch.
To subdivide the mesh more times, simply add the required number of node groups sequentially.