Calculating the angle between two mesh edges in Blender

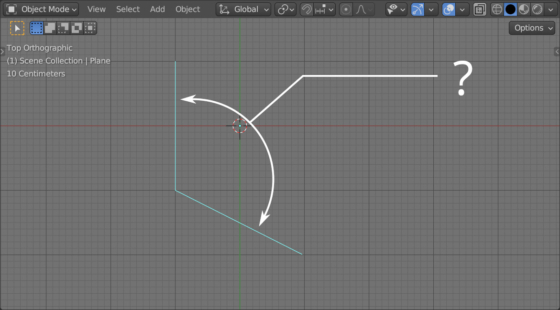
Determining the angle between two adjacent mesh edges is necessary, for example, when searching for elements on the model that are too sharp, or, conversely, not sharp enough.

.blend file on Patreon

To calculate the angle between two mesh edges adjacent to one point, it is most convenient to use the bmesh structure.

Create a bmesh object and load the geometry of the current active scene mesh into it. Bring the indexing of vertices and edges into accordance with the indexing of the original mesh.

Let’s take a point with index 0. Two edges are adjacent to it, between which we want to calculate the angle.

We can get both edges adjacent to a point using its link_edges property:

Now starting from the edges, we can get their common vertex:

and the two remaining vertices:

Now, using these three points, we can construct two vectors corresponding to two mesh edges:

To calculate the angle between two vectors, we can get their dot product, or we can use the angle() function from the mathutils module, which does the same thing.

There are actually two angles between two vectors. Most often, when doing calculations, we need the inner (smaller) of them. The angle() function calculates the angle between vectors in a right-handed coordinate system i.e. clockwise. Accordingly, we do not know exactly what angle we will get as a result. However, we can simply compare the angle with 180 degrees, and if it is greater, then we have found an external (larger) angle. To get the internal one, we need to subtract the resulting value by 360 degrees.

Note that the angle() function returns the result in radians. To operate with degrees, we need to remember to make transformations.

As a result, we will get the angle we need: